Empirical Rule: Definition, Formula, Example, How Its Used
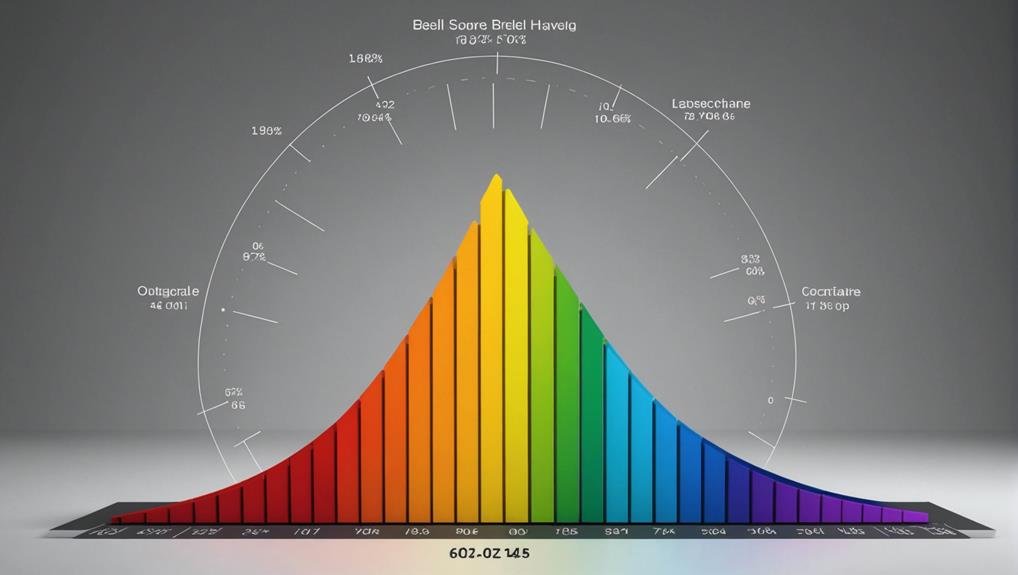
The Empirical Rule is a statistical concept that analyzes data distribution in a normal curve by determining the percentage of data within specific standard deviations. For instance, approximately 68% falls within one standard deviation, 95% within two, and 99.7% within three. This rule aids in interpreting data patterns, supports decision-making processes, and is essential for risk assessments. Understanding this rule is fundamental for statistical analysis and provides valuable insights into data characteristics. Discover more about its formula, examples, and practical applications to enhance your understanding of data distribution and its implications.
Key Takeaways
- Defines proportion of data within standard deviations in a normal distribution
- Indicates percentages within 1, 2, and 3 standard deviations for data interpretation
- Demonstrates data distribution around the mean for decision-making
- Helps estimate volatility, evaluate risk, and make informed choices in finance
- Crucial for forecasting, quality control, risk assessment, and understanding data spread
Empirical Rule Definition
Defining the empirical rule in statistics elucidates the proportion of data within standard deviations in a normal distribution, providing valuable insights into data distribution characteristics. This definition explanation allows for a clear understanding of how data is spread around the mean and helps in data interpretation.
By stating that 68% of data falls within one standard deviation, 95% within two standard deviations, and 99.7% within three standard deviations from the mean, analysts can interpret the distribution of data effectively. The empirical rule sets the foundation for statistical analysis by establishing the expected range within which data points are located, aiding in decision-making processes and risk assessments.
Formula for Empirical Rule
An essential mathematical expression encapsulating the empirical rule in statistics is used to determine the percentage of data within specific standard deviations in a normal distribution.
This formula defines the proportion of data falling within each standard deviation from the mean: approximately 68% within one standard deviation, 95% within two standard deviations, and 99.7% within three standard deviations.
The formula plays a crucial role in statistical analysis and data interpretation, providing a framework for understanding the distribution of data in a given dataset.
Example of Empirical Rule
Utilizing statistical principles, an illustrative application of the empirical rule can be demonstrated through a practical example showcasing the distribution of data within standard deviations from the mean.
For instance, in data distribution analysis, consider a dataset representing the heights of individuals in a population. Applying the empirical rule, we can expect approximately 68% of the heights to fall within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.
This statistical forecasting technique aids in understanding how data is spread around the mean, providing valuable insights for various fields such as quality control, risk analysis, and decision-making processes based on the distribution of data points within specified intervals.
Empirical Rule in Action
In practical scenarios such as investment analysis, the application of the empirical rule can provide valuable insights into estimating volatility and evaluating risk in financial instruments. Through empirical rule analysis, analysts can appraise the likelihood of various outcomes within specified standard deviations from the mean, aiding in decision-making processes.
Real-world applications of the empirical rule extend to evaluating the spread of data around the mean, estimating potential returns, and understanding risk levels in investment portfolios. By utilizing the principles of the empirical rule, financial professionals can gain a better understanding of the distribution of data, helping them make informed choices when managing investments and navigating the complexities of the financial market.
Empirical Rule Applications
Exploring the practical implementation of the empirical rule reveals its significance in data analysis and decision-making processes across various industries. Real-world applications of the empirical rule include forecasting final outcomes, quality control, risk evaluation, and testing distribution normality.
It is frequently used to estimate probabilities, assess risks, and understand data spread around the mean. The rule aids in setting control limits, making rough estimates about future data outcomes, and interpreting large datasets with unknown variables.
In practical scenarios, it assists in estimating the likelihood of events, such as animal lifespans, and plays an essential role in various decision-making processes. The empirical rule's practical implications extend to enhancing data analysis and providing valuable insights for informed decision-making.
Empirical Rule in Finance
The application of the empirical rule in finance involves adapting statistical concepts to analyze and manage investment risks and returns effectively. While market data may not strictly adhere to a normal distribution, analysts utilize tools like standard deviation for volatility analysis in investments.
For instance, evaluating the volatility in portfolios or indices through metrics like daily standard deviation for the S&P 500 aids in investment forecasting. The empirical rule's definition, indicating the percentage of data within each standard deviation in a normal distribution, is particularly relevant in finance for examining stock prices, price indices, and forex rates.
Benefits of Empirical Rule
Understanding the benefits of the empirical rule provides a foundational framework for leveraging statistical insights in decision-making processes across various fields. The table below highlights the key advantages of utilizing the empirical rule in statistical analysis and data interpretation:
| Benefits of Empirical Rule |
|---|
| 1. Provides a structured approach for data interpretation |
| 2. Facilitates quick identification of outliers in datasets |
| 3. Helps in setting realistic performance expectations based on data distribution |
| 4. Assists in making informed decisions by understanding the probability distribution of outcomes |
Conclusion
To sum up, evaluating the empirical rule provides a valuable framework for understanding the distribution of data and setting control limits in statistical analysis. By following the 68-95-99.7 rule, analysts can make informed decisions based on the likelihood of observations falling within a certain range of the mean.
This rule serves as a guiding principle in various fields, including finance, where it helps in estimating volatility and assessing risk in portfolios and indices. Embrace the certainty within uncertainty.